| Definitions | (e <loc e'), A c B, local-state(f;base;X;e), B, local-state(f;base;X;e),  , p , p   q, p q, p   q, p q, p    q, e = e', deq-member(eq;x;L), a = b, a = b, qeq(r;s), q_less(a;b), q_le(r;s), eq_atom$n(x;y), [d] q, e = e', deq-member(eq;x;L), a = b, a = b, qeq(r;s), q_less(a;b), q_le(r;s), eq_atom$n(x;y), [d] , a < , a < b, x f y, a < b, x f y, a < b, null(as), x =a y, (i = b, null(as), x =a y, (i =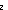 j), i j), i  z j, i <z j, p =b q, constant_function(f;A;B), r z j, i <z j, p =b q, constant_function(f;A;B), r  s, e < e', val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time), s, e < e', val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time), 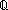 , ,  , Msg(M), kindcase(k; a.f(a); l,t.g(l;t) ), , Msg(M), kindcase(k; a.f(a); l,t.g(l;t) ),   x,y. t(x;y), x,y. t(x;y),   x. t(x), Knd, EState(T), EOrderAxioms(E; pred?; info), Id, IdLnk, Unit, EqDecider(T), E(X), f(x)?z, type List, P x. t(x), Knd, EState(T), EOrderAxioms(E; pred?; info), Id, IdLnk, Unit, EqDecider(T), E(X), f(x)?z, type List, P    Q, P & Q, P Q, P & Q, P   Q, {x:A| B(x)} , Top, Q, {x:A| B(x)} , Top, 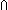 x:A.B(x), tt, x:A.B(x), tt,   b, b,  , ,  , ff, False, Void, case b of inl(x) => s(x) | inr(y) => t(y), t.1, let x,y = A in B(x;y), left + right, X(e), x , ff, False, Void, case b of inl(x) => s(x) | inr(y) => t(y), t.1, let x,y = A in B(x;y), left + right, X(e), x  dom(f), e dom(f), e   X, prior(X), X, prior(X),  A, A,  b, f(a), P b, f(a), P   Q, strong-subtype(A;B), <a, b>, prior-state(f;base;X;e), if b then t else f fi , a:A fp Q, strong-subtype(A;B), <a, b>, prior-state(f;base;X;e), if b then t else f fi , a:A fp B(a), x:A B(a), x:A  B(x), E, AbsInterface(A), Type, ES, B(x), E, AbsInterface(A), Type, ES,  x:A. B(x), x:A x:A. B(x), x:A  B(x), t B(x), t  T, s = t T, s = t |